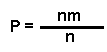
DISTRIBUCIÓN DE POISSON

Esta distribución adquirió su nombre en honor al matemático francés Siméon Denis Poisson, esta distribución se obtiene llevando la distribución binomial al caso límite, es decir, cuando la probabilidad del acierto p tiende a cero (p → 0) y n tiende a infinito (n → ∞ ), de tal manera que el valor de la media es  μ = np y tiende a adquirir un valor finito. 

Esta distribución también tiene su media y su varianza, de tal forma que  σ² = μ o sea que la varianza es igual a la media.

Esta distribución proporciona valores de probabilidad o de probabilidades, por ejemplo cuántos individuos pasan por un punto dado considerando un intervalo de tiempo definido de manera unitaria.

En esta distribución se pueden observar las probabilidades durante la experimentación con eventos que consideran el reemplazo.

Esto se puede explicar mejor con un ejemplo: Dentro de una laguna se tienen n individuos, de los cuales m están infectados con algún tipo de hongo y n - m es el número de individuos que no presentan la infección.

El objetivo del investigador es capturar un individuo escogido al azar de la población de la laguna y la probabilidad de que el individuo capturado esté infectado con el hongo es:

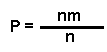
Si en una muestra de n individuos extraídos de la laguna de forma aleatoria y con reemplazo entonces esta presenta una probabilidad p de que sean extraídos exactamente x de los n individuos que presenten la infección, entonces la función de distribución es:

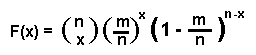
donde n = 0,1,2, ... , n

ya que un individuo muestreado se regresa al estanque lo cual permite que el individuo pueda ser muestreado nuevamente.

Si el muestreo se hiciera sin considerar el reemplazo, o sea, muestreo sin reemplazo entonces la función de distribución para las probabilidades será:

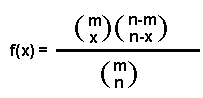
donde n = 0,1,2, ... , n